締合高分子是一類含有可逆非共價相互作用的特殊高分子體系，其中的粘性基體或粘性鏈段（通常稱為“sticker”）可以彼此間以氫鍵、π-π堆積、金屬配位等形式發生可逆的締合反應📶。這些締合高分子具有廣泛的用途💁🏻，不僅可以用於實現諸如自愈合🎥、形狀記憶等功能材料🙋🏿‍♀️，也因其獨特的流變學性質廣泛用於相關領域，如作為流變調節劑使用。因此深刻理解締合高分子的流變現象具有普遍意義。

 目前在不考慮稀溶液條件下的流體力學效應以及高分子纏結效應時，可以通過拓展經典Rouse模型理解締合高分子的線性粘彈性✋。基於高分子體系中應力的分子表達形式，我們指出，從分子層面理解締合高分子體系流變學行為的關鍵在於如何描述一條締合高分子單鏈處於其它高分子鏈背景下的布朗運動。為此我們提出了粘性Rouse模型（Sticky Rouse Model, SRM）🕵🏼，其物理圖景如圖1(b)所示，即考察具有不同運動能力的鏈段在一個均質背景中的運動。運動能力的差異用一個表觀摩擦系數參數δ表示，直接由締合強度決定。

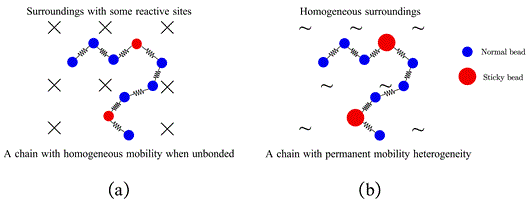
圖1  描述締合高分子鏈布朗運動的兩種物理圖景

 與圖1(a)所示的直觀物理圖景相比，SRM在計算上更為方便，同時又真正將分子層面的結構和運動行為與宏觀力學性能聯系起來，是一個普遍適用的分子理論模型。我們在SRM的框架下開展了大量的理論計算，其中最關鍵的是對運動方程進行簡正化處理，即求出我們所定義的粘性Rouse-Zimm矩陣的本征值與本征向量⏺。通過計算發現，基於SRM不僅可以得到與實驗結果一致的粘彈性函數🖖🏽👳🏽‍♀️，並且進一步通過本征值得到了松弛時間譜的完整信息😴，以及通過本征向量分析出了分子運動模式的變化🌊。這些理論計算的結果為後續的進一步研究提供了關鍵線索。

 為了進一步驗證SRM所預測的理論結果，我們開展了分子動力學模擬研究。通過模擬不僅能方便地表征締合體系中的微觀動力學♘，同時可進一步分析在理論計算中忽略的其他因素。首先考察了模擬體系在不同締合參數條件下的動力學行為👍🏿，通過考察締合弛豫時間τ_sti隨締合強度與反應物濃度的變化關系🕦，確定了在模擬體系中發生的是活化能固定的二元躍遷反應，因此提高粘性鏈段濃度會加快締合反應的速率🏌🏻‍♂️。此外，這一締合反應並不會受到體系凝膠化過程的影響，因此是一個完全由反應動力學決定的過程。

 為了定量比較模擬與SRM理論預測的結果🧱🤹🏽‍♂️，我們通過計算本體中締合高分子鏈的質心擴散系數👤，以及用於示蹤的均聚物鏈在締合基體中的質心擴散系數👵🏻，得到了相對表觀摩擦系數δ的準確數值。通過比較δ和先前得到的締合弛豫時間τ_sti，我們發現二者在完全凝膠化的狀態下的確可以互相轉換，幾乎滿足一致的參數依賴關系，因此SRM利用表觀摩擦效應代替締合鍵壽命的基本思路是成立的🤵🏽👩🏻‍🎓。

        (a)                                                   (b)

圖2 線性松弛模量G(t) 的模擬（散點）與SRM理論預測（實線）比較🧑🏻‍🏭。(a)表示不同粘性鏈段數目，(b)表示不同締合強度。

       基於這一階段的結果👭🏻，我們在不引入任何擬合參數的情況下，通過SRM直接計算出體系的線性粘彈性函數。從圖2的比較中我們可以看到👩🏿‍🦱，二者存在定量一致性❤️！

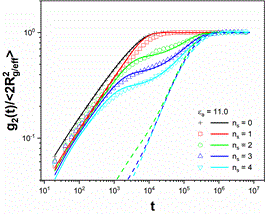
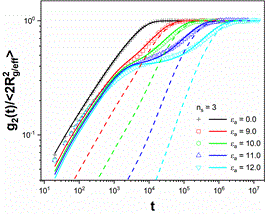
除了宏觀層面上的力學松弛行為，我們進一步比較了分子層面上的弛豫過程，即締合高分子鏈的構象松弛，並提出了表觀質心的概念，以及每個鏈段相對於表觀質心的擴散函數g₂(t)。同樣🧍🏻，不借助任何擬合參數🙎🏽‍♂️，直接通過理論計算得到了與模擬定量一致的結果，如3所示🦮。在進一步分析結構缺陷對力學松弛與鏈段松弛函數的影響時，我們發現引入構象平均並不能顯著提高SRM對G(t)的理論預測精度，但對於g₂(t)卻有十分顯著的效應✌🏻。因此基於SRM可以十分準確地描述出單鏈的構象松弛過程🌤。

          (a)                                                       (b)

圖3 鏈段松弛函數g₂(t)的模擬（散點）與SRM理論預測（實線）比較。 (a)表示不同粘性鏈段數目，(b)表示不同締合強度。

總之🛟🚣🏽‍♂️，我們基於高分子流變分子模型的理論基礎以及對物理圖景的轉換💂🏼‍♂️，提出了具有廣泛適用性，同時又易於計算的粘性Rouse模型SRM。通過定量比較理論與模擬結果✭，進一步證實了🦮：在SRM單鏈理論框架下，可以實現對締合高分子在各個分子層面動力學行為的自洽描述👨🏻‍⚕️，對於進一步深化理解締合高分子體系的流變現象具有重要意義。

 SRM的基本理論框架於2020年發表在Macromolecules上（https://doi.org/10.1021/acs.macromol.0c00312）👨🏻‍🦲，分子動力學模擬的部分工作近期發表在Journal of Rheology（https://doi.org/10.1122/8.0000218）🫅🏼。沐鸣开户2017級碩士研究生蔣諾斐（現為唐萍課題組科研助理）為兩篇文章的獨立一作，通訊作者為唐萍教授與楊玉良教授。